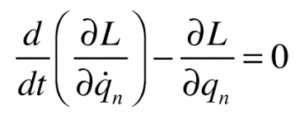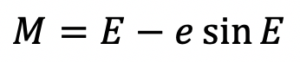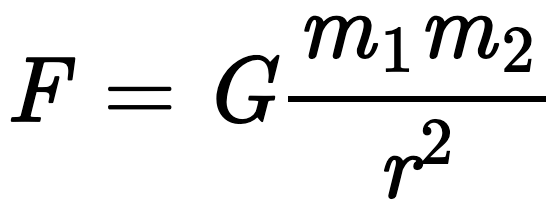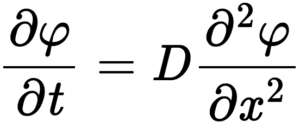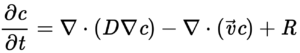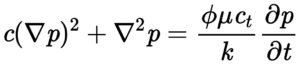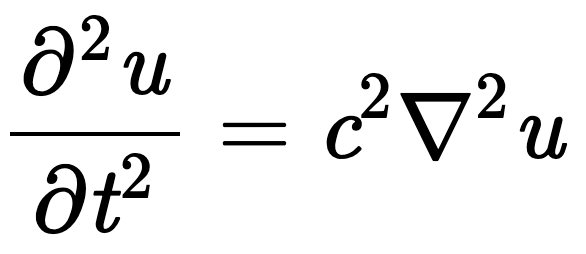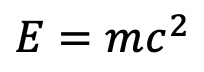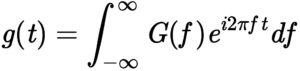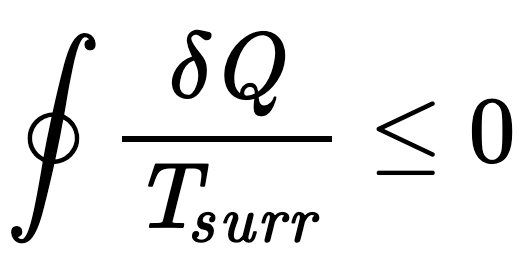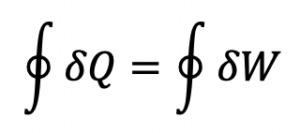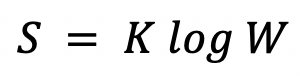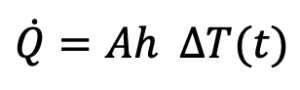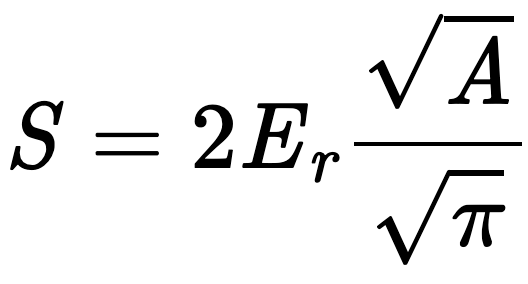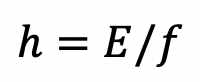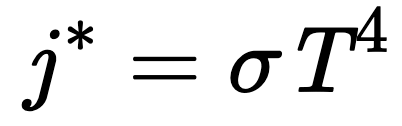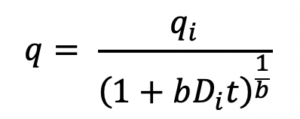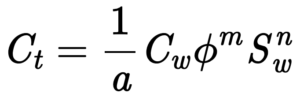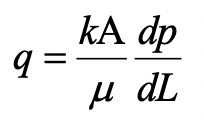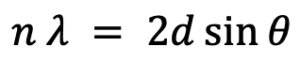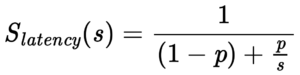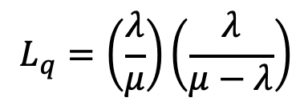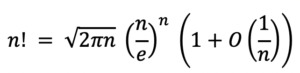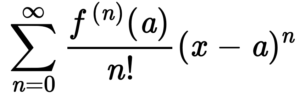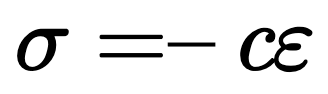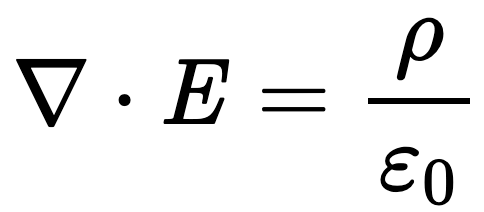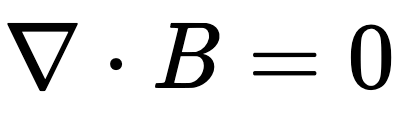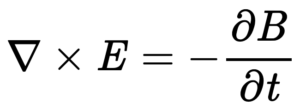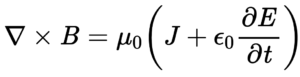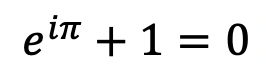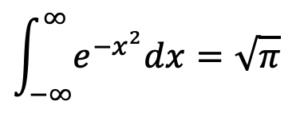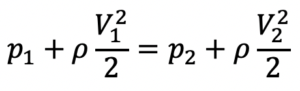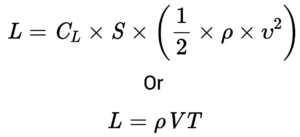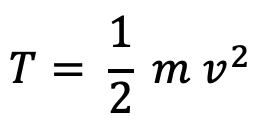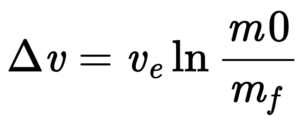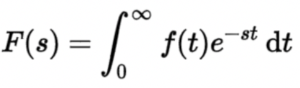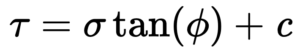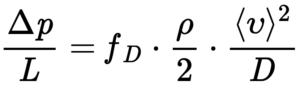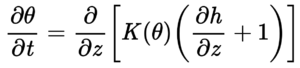1
Ohm’s Law
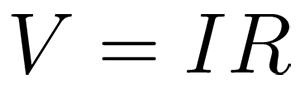
Ohm’s Law states that the current through a conductor between two points is directly proportional to the voltage across the two points.
Related department: Biomedical, and Electrical & computer engineering
2
Bayes’ Theorem
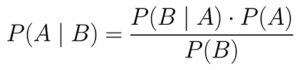
Bayes’ Theorem describes the probability of an event, based on prior knowledge of conditions that might be related to the event.
Related department: Industrial and systems engineering
3
Linear Dynamical System
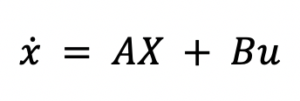
The evoluation of a Linear Dynamical System subject to inputs may be modeled with a first order matrix differential equation. This equation is ubiquitous in engineering.
Related departments: All engineering departments
4
Laplace’s Equation
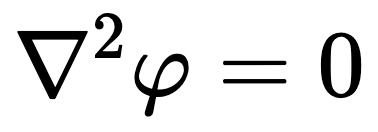
Laplace’s equation is a second-order elliptic partial differential equation. The solutions of Laplace’s equation are important in many fields of engineering, notably electromagnetism, astronomy, and fluid dynamics, because they can be used to accurately describe the behavior of electric, gravitational, and fluid potentials.
Related departments: All engineering departments
5
Navier-Stokes Momentum Equations
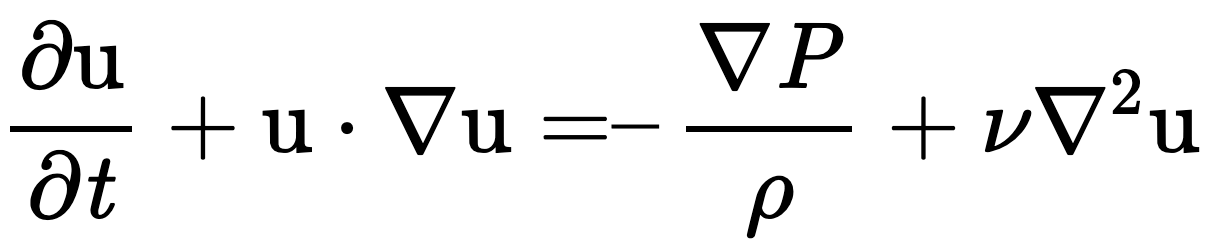
The Navier-Stokes Momentum Equations describe the motion of viscous fluid substances. These equations describe the physics of many phenomena of engineering and scientific interest.
Related departments: Aerospace, biomedical, chemical, and mechanical engineering
6
Cauchy Momentum Equation
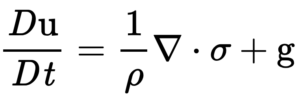
The Cauchy Momentum Equation is a vector partial differential equation that describes the non-relativistic momentum transport in any continuum. Essentially, the time derivative of the flow vector field is related to the divergence of the stress tensor and to the body forces per unit mass.
Related departments: All engineering departments
7
Reynolds Number
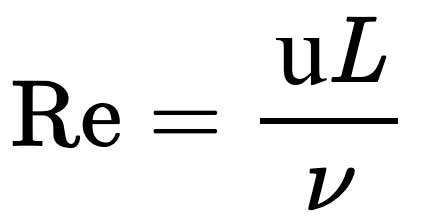
The Reynolds Number is an important dimensionless quantity in fluid mechanics that is used predict flow patterns in different fluid flow situations. It is the ratio of inertial forces to viscous forces.
Related departments: Aerospace, biomedical, chemical, and mechanical engineering
8
Ideal Gas Law
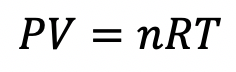
The Ideal Gas Law is the equation of the state of a hypothetical ideal gas. It is a good approximation of the behavior of gases under many conditions.
Related departments: Aerospace, chemical, mechanical, and petroleum engineering
9
Newton’s Second Law of Motion
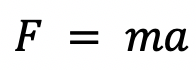
Newton’s Second Law of Motion states that the vector sum of forces on an object equals the mass of the object multiplied by its acceleration for an inertial observer.
Related departments: All engineering departments
10
Lagrange Equations
The Lagrange Equations are a convenient form to model the motion of systems. They may be viewed as a different form of Newton’s second laws. The Lagrange equations are ideal for systems with conservative forces and for bypassing constraint forces in any coordinate system.
Related departments: Aerospace and mechanical engineering
11
Kepler’s Equation
Kepler’s Equation is a transcendental equation that relates the Mean anomaly of orbital motion to the eccentric anomaly and orbit eccentricity for a body subject to a central force.
Related departments: Aerospace engineering
12
Newton’s Universal Law of Gravitation
Newton’s Universal Law of Gravitation states that a particle attracts other particles in the universe through a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between their centers. This is a general physical law derived from empirical observations.
Related department: Aerospace engineering
13
Fick’s Second Law of Diffusion
Fick’s Second Law of Diffusion is a partial differential equation that predicts how diffusion causes a concentration to change with time. It is essentially the Heat Equation.
Related departments: Aerospace, biomedical, and civil engineering
14
Convection- Diffusion-Reaction Equation
The Convection- Diffusion-Reaction Equation for mass transport is a combination of the diffusion and convection equations, and describes physical phenomena where particles, energy, or other physical quantities are transferred inside a physical system due to convection, diffusion and reactions.
Related departments: Aerospace, biomedical, and chemical engineering
15
Diffusivity Equation
Diffusivity Equation for the flow of a single phase fluid in a porous media.
Related departments: Biomedical, chemical, and petroleum engineering
16
Wave Equation
The Wave Equation is a second-order linear hyperbolic partial differential equation for the description of waves as they occur in classical physics. The equation can be used to model sound waves, light waves, and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics.
Related departments: All engineering departments
17
Einstein’s Mass-Energy Equivalence
Einstein’s Mass-Energy Equivalence states that anything having mass has an equivalent amount of energy and vice versa, with these fundamental quantities directly relating to one another by Einstein’s famous formula. The formula arose from special relativity.
Related department: Nuclear engineering
18
The Fourier Transform
The Fourier Transform decomposes a signal into the frequencies that make it up, in a way similar to how a musical chord can be expressed as the frequencies (or pitches) of its constituent notes.
Related department: Biomedical, and Electrical and computer engineering
19
The Clausius Inequality
The Clausius Inequality is a fundamental statement of the Second Law of Thermodynamics. It recognizes that the cyclic integral of heat transfer (Q) between a system at temperature (T) and its surroundings is less than zero for all cases but the idealized case of reversibility. The inequality leads to the definition of the non-conserved property of entropy and the reality of entropy generation in real processes.
Related departments: Aerospace and mechanical engineering
20
The First Law of Thermodynamics
The Mechanical Equivalency of Heat states that the cyclic integral of heat transfer is equal to the cyclic integral of work transfer between a system and its surroundings. It was discovered by Joule in his famous experiments and created the basis upon which Conservation of Energy and the First Law of Thermodynamics were based. It leads to the definition of the property internal energy.
Related departments: All engineering departments
21
Boltzmann Entropy Equation
The Boltzmann Entropy Equation shows the relationship between entropy and the number of ways the atoms or molecules of a thermodynamic system can be arranged.
Related departments: Aerospace, biomedical, and ocean engineering
22
Newton’s Law of Cooling
Newton’s Law of Cooling states that the rate of heat loss of a body is directly proportional to the difference in the temperatures between the body and its surroundings, provided the temperature difference is small and the nature of radiating surface remains same.
Related departments: All engineering departments
23
Fundamental Equation of Nanoindentation
The Fundamental Equation of Nanoindentation developed by Texas A&M University’s George Pharr.
Related department: Materials science engineering
24
Planck Constant
The Planck Constant is a physical constant that is the quantum of action and is central in quantum mechanics. It is defined as the ratio of particulate photon energy and its associated wave frequency.
Related department: Aerospace, and biomedical engineering.
25
Stefan-Boltzmann Law
The Stefan-Boltzmann Law describes the power radiated from a black body in terms of its temperature. Specifically, the total energy radiated per unit surface area of a black body across all wavelengths per unit time is proportional to the fourth power of the black body’s thermodynamic temperature.
Related department: Biomedical, and nuclear engineering
26
Arps Equation
Arps Equation is a mathematical model to forecast future production rates of oil and gas wells.
Related department: Petroleum engineering
27
Archie’s Law
Archie’s Law relates the in-situ electrical conductivity of a sedimentary rock to its porosity and brine saturation. It is an empirical law attempting to describe ion flow in clean, consolidated sands with varying intergranular porosity.
Related departments: Civil and environmental and petroleum engineering
28
Darcy’s Law
Darcy’s Law is an equation that describes the flow of a fluid through a porous medium. The law was formulated on the results of experiments involving the flow of water through beds of sand, and it forms the basis of hydrogeology.
Related departments: Biomedical, chemical, and petroleum engineering
29
Bragg’s Law
Bragg’s Law is a relationship describing the angles for coherent and incoherent scattering from a crystal lattice. Specifically, it describes the condition for maximum constructive interference.
Related departments: aerospace, biological and agriculture, biomedical, and electrical and computer engineering
30
Amdahl’s Law
Amdahl’s Law is a formula that gives the theoretical speedup in latency of the execution of a task at fixed workload that can be expected of a system whose resources are improved. This law is commonly used in parallel computing to predict the theoretical speedup when using multiple processors.
Related department: Computer science and engineering
31
M/M/1 Queue
An M/M/1 Queue represents the queue length in a system having a single server, where arrivals are determined by a Poisson process, and job service times have an exponential distribution. The model is the most elementary of queueing models.
Related department: industrial and systems engineering
32
Linear Programming
Linear programming is a method to achieve the best outcome in a mathematical model whose requirements are represented by linear relationships.
Related department: Industrial and systems engineering
33
Stirling’s approximation
Stirling’s approximation is an approximation for factorials. It is a good-quality approximation, leading to accurate results even for small values of n. It is commonly used in the analysis of algorithms.
Related department: Computer science and engineering
34
Taylor Series
Taylor Series is a representation of a function as an infinite sum of terms that are calculated from the values of the function’s derivatives at a single point.
Related department: Mechanical engineering
35
Hooke’s Law
Hooke’s Law is a principle of physics that states that the force (or stress) needed to extend or compress a spring (or continuum media) by some distance (or strain) scales linearly with respect to that distance.
Related department: Biomedical, and mechanical engineering
36
Gauss’s law
Gauss’s Law relates the distribution of electric charge to the resulting electric field. This law can be expressed in an integral form or differential form: the differential form is shown here.
Related departments: Aerospace, biomedical, and electrical and computer engineering
37
Gauss’s Law for Magnetism
Gauss’s law for magnetism is one of the four Maxwell’s equations that underlie classical electrodynamics. It states that the magnetic field B has divergence equal to zero. In other words, that it is a solenoidal vector field.
Related departments: Aerospace, biomedical, and electrical and computer engineering
38
Faraday’s Law of Induction
Faraday’s Law of Induction is a basic law of electromagnetism that predicts how a magnetic field will interact with an electric circuit to produce an electromotive force. It is the fundamental operating principle of transformers, inductors and many types of electrical motors, generators and solenoids.
Related departments: Aerospace, biomedical, and electrical and computer engineering
39
Ampere’s Circuital Law
Ampere’s Circuital Law relates the integrated magnetic field around a closed loop to the electric current passing through the loop. This law can be expressed in an integral form or differential form: the differential form is shown here.
Related departments: Aerospace, biomedical, and electrical and computer engineering
40
Euler’s Identity
Euler’s Identity is a mathematical expression containing three of the basic arithmetic operations: addition, multiplication, and exponentiation. The identity also links five fundamental mathematical constants.
Related departments: All engineering departments
41
The Gaussian Integral
The Gaussian Integral is encountered in physics and quantum field theory. This integral has a wide range of applications in engineering and science, such as computing the normalizing constant of the normal distribution.
Related departments: All engineering departments
42
Bernoulli’s Equation
Bernoulli’s Equation models incompressible fluid flow and is based on the principle that an increase in the speed of a fluid occurs simultaneously with a decrease in pressure.
Related departments: All engineering departments
43
Lift Equation
The Lift Equation states that the lift force on a body equals the lift coefficient, times the wing area, times one-half of the density of the air, times the square of the velocity.
Related department: Aerospace engineering
44
Kinetic Energy
The Kinetic Energy of an object is the energy that it possesses due to its motion. The standard unit of kinetic energy is the joule.
Related departments: All engineering departments
45
Tsiolkovsky Rocket Equation
The Tsiolkovsky Rocket Equation describes the motion of a vehicle that follows the basic principle of a rocket, which is a device that can apply acceleration to itself by expelling part of its mass with high velocity. The equation relates the change of vehicle velocity to the exhaust velocity and initial and final mass of the vehicle.
Related department: Aerospace engineering
46
Laplace Transform
The Laplace Transform is an integral transform that relates a function of a real variable t to a function of a complex variables.
Related departments: All engineering departments
47
Mohr-Coulomb Failure Criterion
The Mohr-Coulomb Failure Criterion represents the linear envelope that is obtained from a plot of the shear strength of a material versus the applied normal stress. More generally, the Mohr–Coulomb theory is a mathematical model that describes the response of brittle materials, like concrete or rubble piles, to shear stress as well as normal stress. Most of the classical engineering materials somehow follow this rule in at least a portion of their shear failure envelope.
Related departments: Civil and environmental and materials science engineering
48
Darcy-Weisbach Equation
The Darcy-Weisbach Equation is a phenomenological equation that relates the head loss, or pressure loss, due to friction along a given length of pipe to the average velocity of the fluid flow for an incompressible fluid.
Related departments: Civil and environmental and mechanical engineering
49
Richards Equation
The Richards Equation is a nonlinear partial differential equation that models the movement of water in unsaturated soils.
Related department: Civil engineering
50
nth Harmonic Number
The nth Harmonic Number, which is the sum of the reciprocals of the first n natural numbers, can be approximated via the formula shown. This approximation is commonly used in the analysis of algorithms.
Related department: Computer science and engineering